Big O Notation understanding is just one of those things a Software Developer has to have in their toolkit. Understanding Big O Notation is vital for success in software engineer interviews. Most software engineer interview questions will present a problem for which you need to provide and potentially implement a solution, and the follow up questions assess your capability of evaluating the complexity of your solution through Big O Notation.
Big O Notation starts off easy and can feel understandable, then BAM the complexity comes in and it leaves you reeling.
Let's do a dive into Big O Notation, and discuss how you can get acquainted with analyzing algorithm complexity without it leaving you perplexed.
What is Big O Notation?
Big O notation is a mathematical notation that describes a limiting behavior of an algorithm or a function. It uses algebraic terms to describe the complexity of our code.
Why is Big O Notation important to understand?
An engineer's job involves a lot of risk minimization. We always need to scrutinize worst-case scenarios as this is the critical point where an application can be deemed incredible by our users or not worth using.
Big O Notation tells us how our code will scale according to traffic, data, you name it. With an analysis of complexity, we can confidently determine how our code will hold up in difficult scenarios.
If you need more convincing, understand that the company's reputation is at stake if its engineers are not considering the worst-case scenarios. One such example of the disasters that can happen is the Niantic Pokemon Go Fest back in 2017. The Pokemon Go app was all the craze but couldn't live up to its hype. The highly anticipated event, for which users traveled to New York, rapidly turned into a nightmare. The app was crashing, unable to get past the login flow and fans were disappointed, some even angered. The CEO was left to flounder with excuses on stage in front of thousands of upset users. Not a good look!
Anyways, back to Big O Notation.
Where can we apply Big O Notation?
Understand that every line of code has a cost to it. The code we write takes up resources like CPU, memory, and network.
Typically, we use Big O Notation to describe
- Time Complexity (CPU usage)
- Space Complexity (Memory usage)
For the purposes of this article, I will focus on Time Complexity given it is the more focused subject, especially for interview purposes.
What I will say about the two, however, is know that time complexity and space complexity are two concepts always at war with each other. We as developers have to examine our end goal when writing our algorithms and make a compromise, time complexity versus space complexity.
I plan to write more on the time complexity vs space complexity challenges in another article, subscribe to my newsletter for when that next article comes!
Common Time Complexities
Let's focus on the most important complexities to understand, as well as learn how we can determine which complexity our algorithms fall into.
The most common Big O Notations are:
- O(1) or Constant time complexity
- O(log n) or Logarithmic complexity
- O(n) or Linear time complexity
- O(n²) or Quadratic time complexity
This list of complexities starts from the BEST and goes to the worst.
How about we go through each of them?
O(1) or Constant Time Complexity
When we say that something is written as O(1), this means that it will always execute in constant time. There is no improvement beyond O(1) time complexity (aside from doing nothing at all).
An O(1) Big O Notation time complexity typically falls under array indexing, or operations like push and pop to an array because they are simply adding/removing an item from the tail end of the array.
Array indexing and appending/removing from the end are not operations that can be improved, therefore they fall under O(1) time complexity.
Retrieval of keys from Javascript objects also are of O(1) time complexity.
This knowledge is very important to retain, because many algorithms can be improved by storing data in arrays/objects and the retrieval can be done in constant time (at the expense of space/memory of course, see the tradeoffs?).
Note that O(log n) is indeed faster than O(n), but it is a little more complex to understand. I want to discuss O(n) and O(n²) time complexity first and then we will lastly review how O(log n) is even better than both!
O(n) or Linear Time Complexity
O(n) time complexity is strictly proportional to the size of our input data.Let's say we have an array of size 5.
const arr = [1, 2, 3, 4, 5];
If we wanted to print all of the contents of the array, we would have to iterate through it in a for loop. We would see 5 console logs for each item in the array, which is of O(5) complexity. If the array were of size 10, then we would see 10 logs that make for O(10), and we can keep going with this pattern.
The key takeaway note for this exercise is that the amount of execution is strictly proportional to the size of our array. To abstractly define the number of items in our arrays, we can refer to them as n items.
This leads us to generalize the time complexity, where we could say an algorithm/function that runs through all the data in a linear fashion has a time complexity of O(n).
Let's look at an example of a function with O(n) Big O Notation time complexity.
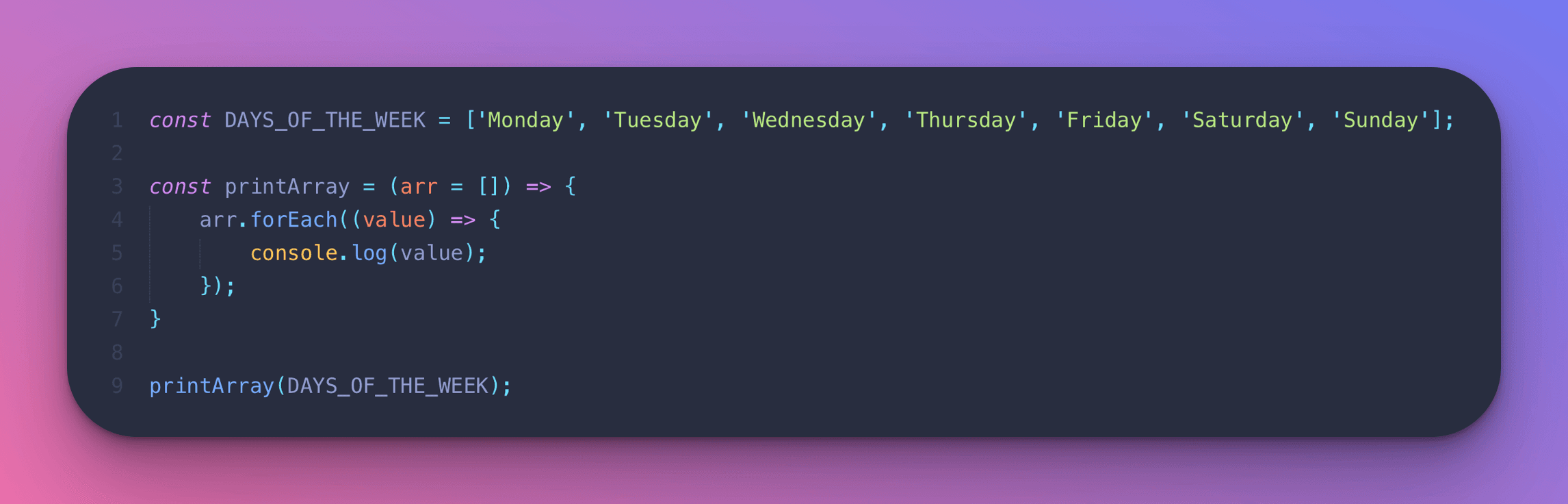
The following printArray function has a time complexity of O(n) because it can take an array of any arbitrary length and always iterates through it in a for loop to print every value.
Now I gave away the circumstances in which we would have an algorithm/function with a runtime of O(n). Typically we observe time complexity of O(n) when we iterate through a single array, or if we are using recursion to go through every single item in a data structure, object or array, what have you. Think of recursion as an array.
Recursive functions leverage the "the call stack." When a program calls a function, that function goes on top of the call stack. And a stack behind the scenes is a glorified array, represented by this data structure with added functionality.
Now, this algorithm works if our input size is small. Like my earlier example, 5 or 10 items would be quick to iterate through. However, the time duration gets longer as our list of items grows.
O(n) Big O Notation means that our algorithms take proportionally longer to complete as our input grows.
Remember, our job is to understand the implications of the code we write in the worst-case scenarios. Imagine if we had a million items. We would have to iterate through each one! That can be pretty demanding.
Sometimes we have no choice but to do the O(n) solution, other times we can do better. It's up to the engineer to find a better solution if it is out there.
Now you might at this point be wondering about the code written inside of our for loops or recursive functions. Don't they have a time complexity as well? Absolutely they do!
It's worth mentioning when evaluating Big O Notation that we want to generalize our analysis strictly to the worst-case scenario. Unless the code written in the for loop is WORSE than O(n), the time complexity of the inner for loop logic can effectively be ignored for a time complexity deduction.O(n²) or Quadratic time complexity
Now that we understand O(n) Big O Notation a little bit better, we can see how we might get an algorithm that is O(n²) or even O(n³).
We know that for loops that iterate through all n items have a time complexity of O(n). So ask yourself this, what happens if we iterate through the array twice, through a nested for loop?
Following the thought process for O(n), we know we have an array of arbitrary length that was generalized as n. Now what we are saying is that for each item i in that array of arbitrary length n, we are going to iterate through each item again n times!
This is how we reach the time complexity deduction O(n*n) or better known as O(n²).
Let's look at another example to reach better clarity. Square matrices are the perfect example to demonstrate this time complexity. A matrix is a set of values laid out in tabular form (in rows and columns). We represent a matrix with an array comprised of nested arrays.
In the following code, we define a function that will log the values found in a square matrix of arbitrary size n*n.

I want to raise the following point that I'm iterating through a series of arrays that are guaranteed to be the same length. This is how we can confidently say our time complexity is of O(n²).
If we were to say iterate through one array of a specific size, and have a nested for loop for an array of a different potential size, then technically our time complexity is different. Let's say our first array is of length n, but the second that could be a different size is m.
Our runtime would then be O(m*n).
Here is an example of an algorithm with runtime O(mn) to bring better clarity.

The time complexity for printNestedArraysInOrderis O(mn) Big O Notation because the array DAYS_OF_THE_WEEK is different in length than WEEKS .
We provide this time complexity because printNestedArraysInOrder is written in such a way that it accepts arrays of different lengths and iterates through them in a nested for loop.
Typically we do not want to accept algorithms or functions with a time complexity of O(n²) unless we know that the number of items cannot go to infinity. In an interview setting, we often find that we can easily determine an algorithm of O(n²), and these such answers are known as Brute Force algorithms.
A Brute Force algorithm is a straightforward solution to a problem that heavily relies on computing power. The computer's capability to try every possibility before arriving at an answer gets taken advantage of when instead one could derive more advanced solutions to reduce compute strain.Brute force solutions typically are not necessary! Rather there exist more advanced techniques to dramatically improve efficiency. Time complexity serves as the tool to help us understand just how drastic that change can be.
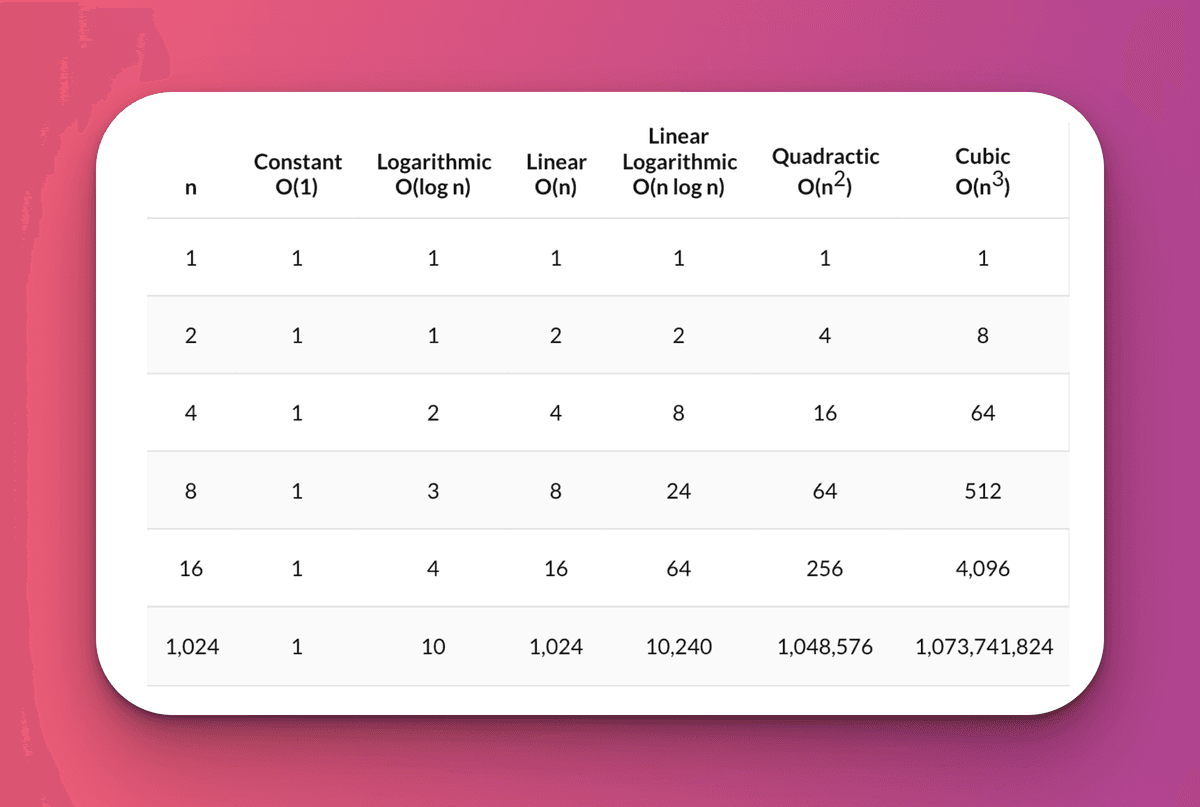
We have not yet discussed time complexity O(log n). However, I want to briefly look again at this chart I attached earlier. Observe just how many steps an O(n²) time complexity algorithm takes if n is of length 1,024.

For an O(n²) time complexity we observe over 1 million rounds to arrive to a conclusion! Furthermore, we see how O(n³) is absolutely atrocious. The amount of iterations required to arrive at a solution quickly gets out of hand.
But, looking at O(log n) the results are incredible! For the same 1,024 value, we see that only 10 steps at most are required to arrive at a solution. This is as close as we can get to a time complexity of O(1), better known as the best time complexity possible.
O(log n) or Logarithmic complexity
We finally arrive to the last time complexity, which can be among the more difficult to understand.
The O(log n) Big O Notation which we will be considering for these examples is that of the binary logarithm.
The binary logarithm is of base number 2. Binary logarithms are the basis for the binary numeral system and are critical to computer science. The binary logarithm is the basis for all binary code used in computing systems. It allows us to count using zero and one numbers only.With that, let's dive in!
The way I like to explain the O(log n) complexity is by example of a famous algorithm.
Let's explain the problem statement and solution for the binary search algorithm.Binary Search Problem Statement
Imagine we have an array of arbitrary length. We want to find if a particular value exists in said array.
The lack of awareness of the actual values in the array is a plausible real scenario. When dealing with data we often do not necessarily know all the contents of said data. So, how do we find this desired value in the most optimal way?
Binary Search Approaches for a Solution
Our brute force solution could be to simply iterate through the entire array, and see if we observe this value. This time complexity at its worst, as we discussed earlier is O(n). Data often however is comprised of millions of entries, so this is not a practical solution.
This is where for binary search, a more advanced algorithm comes into play to save the day.
Binary search starts by assuming that we sorted the array. Note that sorting can be done in O(log n) time. Knowing this, we can rest assured that so far we are not harming the integrity of the time complexity of our solution by starting off with sorting.
Now we get to the general idea of the binary search algorithm. Let's say our sorted array looks like the following example:
const arr = [1, 4, 7, 11, 20, 22];
Let's say we want to find out if the number 4 is in our array. The idea behind a binary search involves asking the question: What we can do is split the sorted array in half, take the middle number and observe if it is smaller, or bigger than our desired number. If the middle value is equal to 4 then great, we found our desired number and can return as it is indeed in the array. If we find the middle is a number that is smaller than what we are looking for, we can disregard the left half of the array from that selected midpoint. Why? Because we know the array is sorted! Any number further to the left will guaranteed to be smaller than the middle and we already know the middle is smaller than the value we are looking for. So we can safely proceed to the right for the rest of our search. We can likewise apply the same logic for numbers larger. If we see that the middle is larger than what we are looking for, we know the numbers to the right are sorted and also larger! So we can proceed to the left for the rest of the binary search. After we choose a direction, we split the problem in half again and continue on until we find our desired value.
The strategy behind the binary search solution involves splitting subsets of the problem in half repeatedly until we arrive at an answer. Each iteration results in elimination of many values we would have otherwise been forced to waste a check on should we have performed an O(n) linear search solution!
The binary search approach utilizes the Divide and Conquer strategy. Most Divide and Conquer capable questions involve time complexities of O(log n).
A divide and conquer algorithm is a strategy of solving a large problem by breaking the problem into smaller sub-problems, solving those sub-problems and combining them to get the desired output.If you want to better understand how we arrive to O(log n) for this solution, let's dive in. What does log n do?
Let's evaluate values where:
n = 2^x, and x = {1, 2, 3, 4, 10} (Note that I skipped values in the x set for sake of example, from 4 - > 10)
Our resultant values for n are:
n = {1, 2, 4, 8, 16, 1024}
When we put n into our log(n) function, we arrive to values
log (n) = {0, 1, 2, 3, 4, 10}
Notice the results are not exactly half. If you think back to the divide and conquer algorithm this might make a little more sense. We only divide the problem in half once, then we divide a subset in half, and so on. We aren't necessarily halving the whole problem, we are halving halves repeatedly, so it's even better than halving our solution.
Now we can hopefully see why the binary search problem can be tackled by a divide and conquer algorithm.
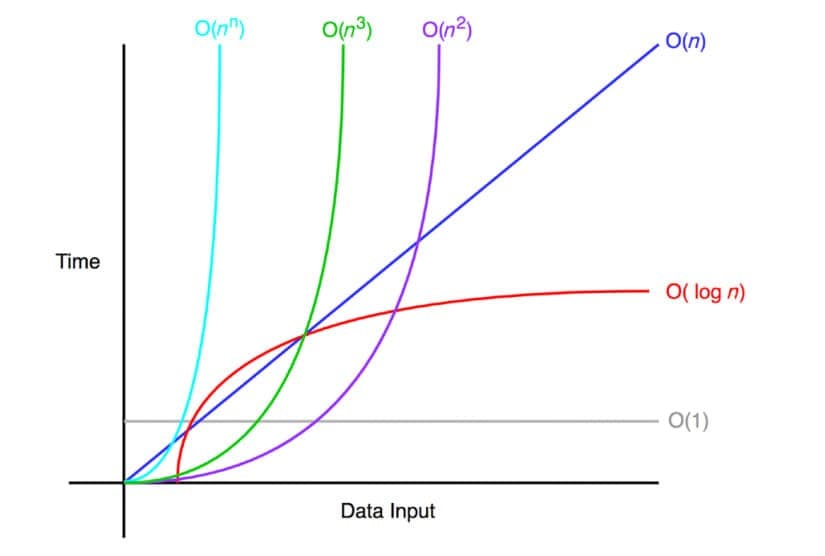
Now we can maybe start to see how dramatically different log (n) performs against the other time complexities we went over.
We saw that O(n) Big O Notation is strictly equal to the number of elements. That is why we see the diagonal line. For every x, we see the same y.
O(n²) however we saw earlier in our chart gets worse as n grows bigger, and O(n³) gets out of hand even quicker. Looking at the graph, we see this in the visual representation as the line races vertically high up when given much smaller values on the x-axis of this graph.
Now O(log n) however, stretches out nicely as the values along our x-axis gradually get larger. Yes, it is moving vertically upwards, but at a much slower rate.
This is why a time complexity of O(log n) is much better than the other solutions we reviewed.
Finally, observe how O(1) time complexity is unbeatable. It can't get any better than that!
Hopefully, now you can see how critical it is to be able to evaluate time complexities in the code we write. It is invaluable to write algorithms that spend less computing power as it inevitably results in a faster response.
We all know that Fast = Sleek!
Ultimately, understanding Big O and the capacity to optimize algorithms make for the difference between an acceptable engineer who can do the job and a phenomenal engineer who can excel at the job.Happy coding everyone!
Remember, developers are creatures that turn coffee into code. So I'd very much appreciate if you bought me a coffee!  I’m a new writer and I will be posting very frequently on my findings and learnings in the tech industry and beyond. Join my newsletter if you would like to stay tuned!
I’m a new writer and I will be posting very frequently on my findings and learnings in the tech industry and beyond. Join my newsletter if you would like to stay tuned!
Thanks for reading again! ❤️
| Understand Open Graph Dynamic Image Meta Tags | 1 |
| Pros and Cons of Caching Data in Software | 2 |
| How to build a Modal in ReactJS (Part One) | 3 |
